人工智能的另类途径:涌现计算
近日,凯文·凯利(Kevin Kelly,简称KK)很火。其实,KK在中国的走红与国内诸多互联网大佬们的吹捧不无关系。现如今,去中心化、自组织、生态系统等词汇已然成为了互联网公司信奉的金科玉律,而它们恰恰大多来源于KK的那本成名之作《失控》。这本书自始至终都在谈论一个主题,这就是复杂系统。
事实上,早在20世纪的70-80年代,科学家们就已经将关注的焦点定位在各式复杂系统之上,而涌现则是复杂系统中最显著也是最重要的一种特征。涌现(Emergence),字面翻译为突然出现,在系统科学中它意味着“整体大于部分之和”。任何系统都是由大量微观元素构成的整体,这些微观个体之间会发生局部的相互作用,然而当我们把这些个体看作一个整体的时候,就会有一些全新的属性、规律或模式自发地冒出来,这种现象就称为涌现[1]。
一个涌现的实例来自都市中闪烁的霓虹灯。我们知道,霓虹灯那色彩斑斓的图案无非是由上百支灯泡闪烁而形成的。在灯泡的层面,我们找不到高层次的图案或文字,因此图案和文字就是涌现结果。另一个例子来自蚂蚁王国[2]。我们都知道,每只小小的蚂蚁是一个非常简单的个体,它们没有聪明的头脑,只会完成一些简单的任务。然而,当把成千上万只小蚂蚁组合到一起的时候,整个蚁群就能体现出非常复杂、庞大的涌现现象,例如社会分工、集体协作等等。
例如在蚂蚁觅食的活动中,它们就能体现出涌现的行为。我们知道,单个的蚂蚁由于体形弱小,所以它们的视力范围非常有限,只能看到邻近的景物。然而,当大量的蚂蚁共同协作的时候,它们通过相互作用传递信息,就可以发现一条最快的搬运食物回巢的路线。那么,这条最快的搬运路径就是典型的蚂蚁群体的涌现行为。而且,我们知道,在这群蚂蚁中,并没有哪个蚁王或者蚁后对整队蚂蚁发号施令,所有的涌现行为全部是这群蚂局部相互作用的结果。
那么,我们能否借鉴涌现的思想,来设计出一些人造的系统或程序,从而为我们人类服务呢?这就是涌现计算要解决的问题。将涌现的思想借鉴到计算系统中来便构成了涌现计算的想法。从计算的观点来看,一个涌现系统其实就是一个并行计算的系统。蚁群中的单个蚂蚁就是一个小型的处理器,它们可以并行地、局部地完成计算任务。那么蚁群、霓虹灯整体就可以通过集合这些并行处理单元,而完成复杂的运算任务,例如寻找到有效的搬运食物路径或者形成复杂好看的图案。我们完全可能设计一个人工计算系统来通过模拟简单的并行计算单元而实现整体涌现系统的模拟。
例如,我们可以把蚁群觅食的例子用计算机模拟出来[2]。如下图所示:
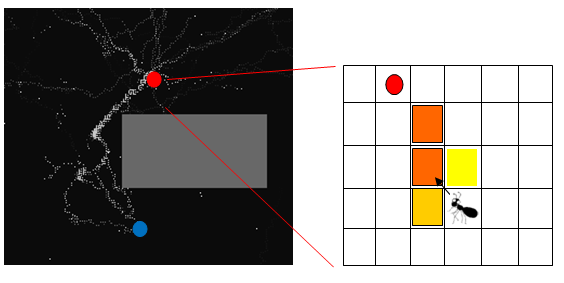
图1:蚂蚁觅食的计算机模拟,白点表示蚂蚁,灰点表示信息素,红点表示食物,蓝点表示巢穴,灰色的方框是障碍物,将红点附近的区域放大得到右图。可以到 http://www.swarmagents.cn/javaclass/ant.htm 观看模拟结果。
在一个二维的、离散化的网格世界里,我们可以用一个计算机程序体(称之为Agent)来模拟一个觅食的蚂蚁。这只蚂蚁可以从自己的巢穴出发,在这个网格世界中随机游走,如果它找到了食物就开始往回折返。为了呼唤其他的蚂蚁过来,它会往经过的格子中撒下信息素(右图中的彩色方格)。其它的蚂蚁在随机游走的过程中,如果碰到了彩色的方格(闻到了信息素的味道)就会沿着信息素的浓度引导向前爬行,直到找到食物。一旦它找到食物,就又会进一步往环境中播撒信息素。这样,一旦有一只蚂蚁找到了食物,就会吸引更多的蚂蚁过来。
与此同时,信息素会在环境中慢慢地挥发、退色,这样,没有什么蚂蚁经过的那条路径就会逐渐耗散它的信息素。渐渐地,只有那条最短的路径会聚集最多的蚂蚁,蚂蚁群体们就通过相互作用找到了最短的路。所有这些现象完全可以在计算机模拟世界中计算得到。因此,我们说,涌现是可以通过多主体计算进行模拟的。
由于涌现的系统有很多优越特征,例如它的抗干扰能力、创新性等,所以人们感兴趣的是另外一种思路,也就是我们给系统预设一个具体的计算目标,但是这个计算目标不是通过传统的编程直接告诉计算机如何实现,而是通过设计一种微观个体的相互作用规则,而让最终的目标自发地涌现出来。也就是说,如果某系统的涌现行为或者属性可以看作是某种计算的话,那么我们就称这个系统正在执行涌现计算[3]。
涌现计算与涌现的模拟有很大的相似性:它们都是利用计算系统实现系统的涌现现象。但是两者又有很大的不同:涌现的模拟旨在用计算机模拟一个真实的系统,使得这个模拟具备某种涌现的特征;然而涌现计算则要求更高,它要求该系统不仅仅需要具备涌现特征,而且这种涌现特征还能完成某种特定的计算任务。也就是说,涌现模拟是利用个体的简单计算而实现涌现,涌现计算则要求系统的涌现完成实际的计算。
让我们再回到蚂蚁的例子上来。虽然我们已经可以把蚁群的行为和涌现属性用计算机模拟出来了,但是这个模拟系统并不能帮我们执行有意义的计算。
然而,1992年Marco Dorigo在他的博士论文中提出的蚁群优化算法(Ant Colony Optimization)就是一种典型的涌现计算的例子[4]。因为蚁群算法通过改造蚂蚁的模拟程序的确可以找到一条真实地图上的最短路径,因此,作为一种涌现的结果,这条最短路径是被涌现计算而出的。
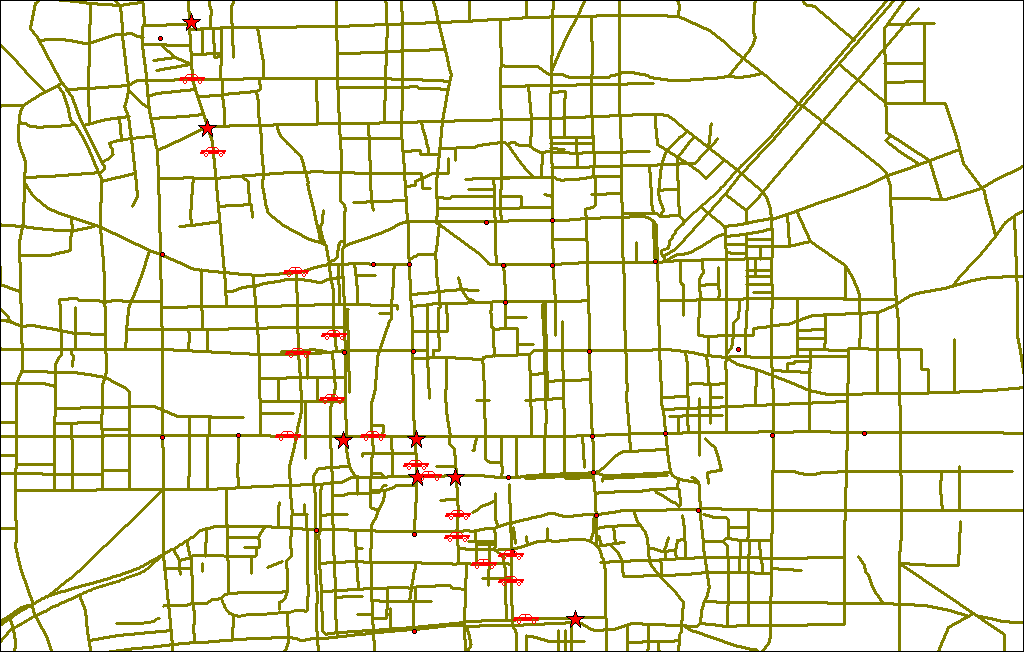
图2:利用蚁群算法计算的真实的最短路径[5],该地图为北京市地图。
进一步,蚁群优化算法还可以被用来解决包括旅行商问题、组合优化问题等更一般的问题上来。这也体现了涌现计算的强大优势。
下一次,我将具体谈谈涌现计算可以解决的各式各样的实际问题,让大家切实感受一下涌现计算是一种何等强大的资源。
文章来源:赛先生
